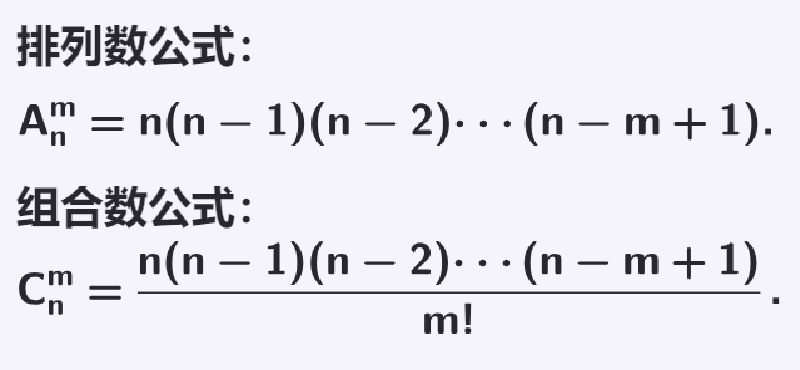排列组合
组合数学中的基础概念
条目
历史版本
排列（英文：arrangement）与组合（英文：combination）是组合学中的基本概念之一。一般地，从
个不同元素中取出
个元素，并按照一定的顺序排成一列，叫做从个不同元素中取出
个元素的一个排列。从个不同元素中取出个元素作为一组，叫做从个不同元素中取出个元素的一个组合。[1][2]
印度有着世界上组合规则的最早记录。约公元前600的苏斯鲁塔（Susruta） 的医学论文中给出了从六种不同的味道物品中分别取
种的组合方法。公元前300年左右，印度耆那教的文献已提到排列组合，并给出了三个排列数和三个组合数。约公元850年数学家马哈维拉（Mahavira）给出了个物体中每次取
个的取法数的一般完整组合公式，可以表述成现代的公式
。1150年印度数学家巴什迦罗（Bhaskara Ⅱ）又给出了
，这是构成算术三角形的基本规则。随着印度的数学成就向西方渗透，1321年莱维·本热尔松（Leviben Gerson，1288-1344）给出了印度已知的3个主要规则：个物体的排列数公式； 个物体中取个的排列数公式；个物体中取个的组合数公式。[3]
组合数具有奇偶性等经典性质，与排列组 合相关的概念是二项式定理，在解决问题时往往需要结合使用。[8][9][10]历史上出现了很多组合学名题，包括八皇后问题、旅行家问题、欧拉三十六军官问题等。[11][12][13]此外，排列组合问题包括多种类型，如相邻问题，捆绑问题
，它还可以用于解决生物、化学领 域的计数难题，是一项重要的数学工具。[5][6][14][15]