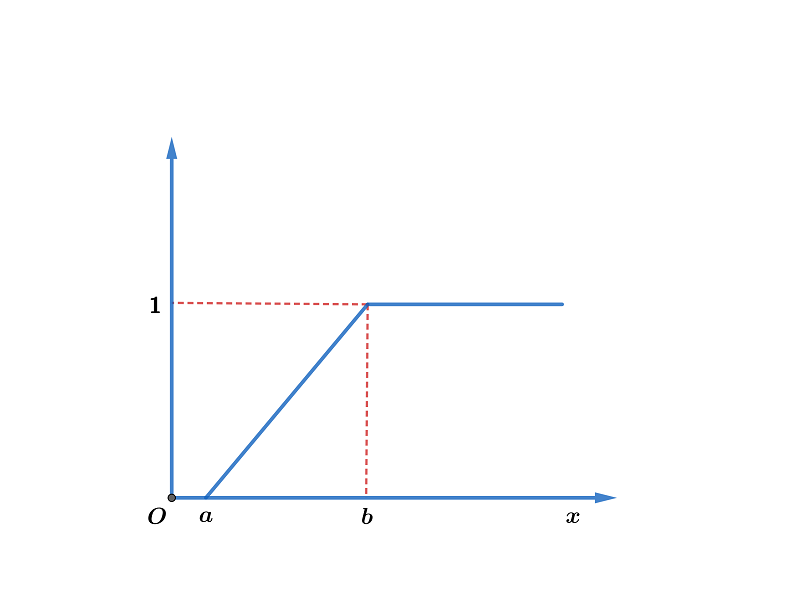
均匀分布
统计学中一种常见的连续型随机变量的分布
条目
历史版本
均匀分布的历史与等可能性思想的形成密不可分。概率论概念的形成最早可见于16世纪，概率是一个事件发生，一种情况出现的可能性大小的数量指标，介于
与
之间。1657年，数学家惠更斯（英文：Huygens）出版的概率论著作《机遇的规律》中，从关于公平赌博的值的一条公理出发，推出了关于“期望”的3条定理，并可在书中前几个命题见到等可能性的思想。后来，1713年著名数学家伯努利（英文：Jacob Bernoulli）所著《推测术》一书出版，书中把古典概率中“等可能性”的思想推广到主观概率的场合，当没有任何理由可以认为众多可能性中的某一个或某一些比其他可能性更具优势时，应给予这些可能性以同等的主观概率。如某个未知量
取值区间在
之内，
取区间内任一值有同等的可能性，即取内的均匀分布
为的主观概率分布，被称为“同等无知原则”，在数理统计史上有着重要的意义。[4]
均匀分布有几个基本性质，包括数学期望，方差等数字特征。[8]它与其他常见的连续型分布有着重要的联系，[9]如正态分布、韦布尔分布、指数分布、贝塔分布等。[3][10]若增加随机变量的个数，均匀分布还可推广至多维。[11][12]同时，它作为一种重要的统计工具不仅能处理一些现实生活的问题，如候车问题等，[5]还可以广泛地应用于遗传学、计算机等其他科学领域，如在现代计算机技术中，均匀分布是蒙特卡罗方法的理论依据，并且在数值计算中，定点计算的舍入误差可作为均匀分布的随机变量。[6][7]